Построение описательной экономической модели.
Данная работа будет посвящена анализу связи между количеством абонентов в сети, средней ежемесячной выручкой от продажи услуг в расчете на одного абонента (ARPU) и чистой прибылью оператора связи на конец отчетного периода.
Исходя из сделанного предположения строим эконометрическую модель
, которая относится к классу факторных статических моделей:
y=f(x1, x2)
где x1 - количество абонентов в сети (объясняющая переменная)
x2 - средняя ежемесячная выручка от продажи услуг в расчете на одного абонента (ARPU) (объясняющая переменная)
y - чистая прибыль (зависимая переменная)
Чтобы убедиться в том, что выбор объясняющих переменных оправдан, оценим связь между признаками количественно, для этого заполним матрицу корреляций:
Таблица 2. Матрица корреляций между исходными статистическими признаками
|
x1 |
x2 |
y | |
|
x1 |
1 |
-0,97 |
0,72 |
|
x2 |
-0,97 |
1 |
-0,71 |
|
y |
0,72 |
-0,71 |
1 |
Анализируя матрицу корреляций, можем сделать вывод о наличии сильной положительной связи между количеством абонентов и чистой прибылью оператора. В то же время также существует сильная отрицательная связь ARPU и чистой прибылью.
Для дальнейшего исследования модифицируем модель к виду парной регрессии: y=f(x1).
Для выбора функциональной формы модели проанализируем корреляционное поле:
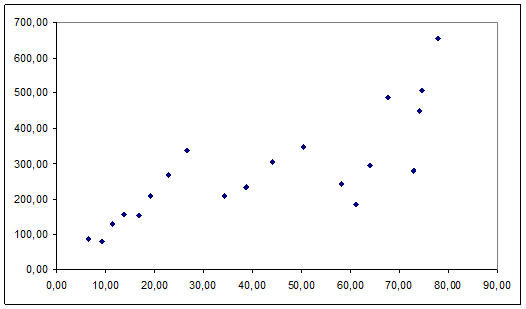
Рисунок 2. Корреляционное поле (x1 - кол-во абонентов в сети, млн. чел.; y - чистая прибыль оператора
Визуальный анализ показывает, что для построения модели вполне подойдет степенная функция:
![]()
Для дальнейшего исследования приведем наше уравнение к линейному виду. То есть:
![]() ,
,
где 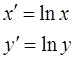 .
.
Таким образом, все дальнейшие исследования будем проводить с этим уравнением.
Оценка параметров модели.
Проведем оценку параметров модели при помощи различных способов.
Метод средних.
Предположим, что изменение чистой прибыли обусловлено только изменением количества абонентов (т.е. α0 = 0). Тогда оценка a1 и a2 неизвестного параметра α1 и α2 определится по формулам:
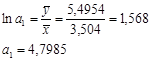
![]()
Тогда модель принимает вид: y=4,7985×x1,35881+e.
Метод выбранных точек.
Проанализируем корреляционное поле и выберем точки, которые ближе всех лежат в предполагаемой прямой линии, описывающей модель. Это будут точки 4 кв. 2004 г. (209,1; 34,22) и 2 кв. 2007 г. (507,9; 74,67).